初中数学课堂中多元评价的应用
新市初中
何小跃
摘要 随着新课程的推进,对学生学习的多元评价得到教师的共识,结合初中数学多个案例探究多元评价。
关键词 课堂评价 多元化 学习兴趣
评价是初中数学的重要激励手段,教师的评价直接影响了学生的行为发展,它将学生与教师的情感、思维有效地联系起来,学生的心理活动直接受到评价的影响。为了更好更全面了解学生的学习过程,增进学生的学习兴趣、提高教师的教学效果,很有必要建立有效的评价目标多元、评价方法多样的评价体系,下面通过几例谈一谈初中数学课堂教学中多元评价的应用。

返回马鞍山初中研究会专题
一、珠联璧合-----及时评价与延时评价
心理学认为:人在轻松愉悦的环境中,能接受更多的知识,更高效地学习,所以说在民主、和谐的课堂氛围里更容易激发一个人的创新欲望。很多教师对学生所回答的问题、所做的练习、学生的板演及时进行评价,可以说是一种有效促进教学目标实现的教学手段。
课堂中非要一律都得及时评价吗?“无声”尚可胜过“有声”,延时评价有时能给我们带来意想不到的效果。笔者在教学一线中经常有这样的体会:组员在活动结束发言过后,教师不要急于一时地评价,而鼓励他结合其他成员的想法再组织,再创造,从而获得更全面细致的结论。这样更利于培养学生多角度地去思考问题,更利于培养学生的发散性思维、求异思维。
案例1:
 如图,已知D、E在BC上,AB=AC,AD=AE,求证:BD=CE. 如图,已知D、E在BC上,AB=AC,AD=AE,求证:BD=CE.
生1:欲证BD=CE,可以考虑用 △ABD≌ △ACE,因为AB=AC,
所以∠B=∠D,AD=AE,所以 △ABD≌ △ACE,所以BD=CE
师:(感到与自己的思路不一致,显的不耐烦)你用全等来证明两条线段相等,思路很好,但凭这三个要素能得到想要的全等吗?请其他同学思考,找到正确的解法。
这是在课堂上经常出现的一幕,其实否定不如引导,最好应用延迟性评价,给生1第二次机会,让他意识到错误的原因,必要时可以适当提示,体现教师对学生情感方面的关怀,另一位教师是这样处理的:
师(面带微笑,舒缓的口吻):建议你看一下△ABD中的三个元素是什么关系,是两边夹一角吗?
生1(很珍惜来之不易的“二次机会”,若有所悟)由AD=AE,得∠ADB=∠AEC,由∠B=∠C,AB=AC,可得△ABD≌△ACE。
师(面带赞许的目光,趁热打铁):用AAS的方法进行全等判定,思路很棒!有没有别的方法?
生1(受到了鼓励)利用"等腰三角形底边上的三线合一"这一重要性质,即过点A作底边上的高AF,由AB=AC得BF=CF,由AD=AE得DF=EF,则BD=EC
同学们爆发出热烈的掌声,这是对生1的肯定与智慧的欣赏,这一刻生1体验着成功的喜悦。正当教师准备结束这道题的讲解时,可喜的状况又出现了:
生2:即然可以证全等,我们也可以用AAS证出△ABE≌△ACD,得BE=CD,从而BD=EC。
生3:也可用“叠合法”来证明:等腰三角形是轴对称图形,顶角的平分线所在直线就是它的对称轴,这样点B与点C沿对称轴折叠必定重合,点D与点E也重合,所以BD=CE
教学随想 本案例中,教师觉得同学1并没有按照自己预设的“情节”走下去,语言中透露出不耐烦,这会让生1的情绪低落,兴趣可能会被大大挫伤,虽然有后面的学生给出了很好的方法,但生1很可能会沮丧消沉,势必影响到其他学生“谨言慎行”,与其说错,还不如“沉默是金”,等待教师的“自导自演”。而另一位教师巧妙地运用延迟评价,给同学们创设了一个民主宽松的环境,体现了教师的教学机智,又使生2在心情放松的情况下说出解决问题的思路,促成生3的思考,有效地训练了学生的发散性思维,如此课堂才会精彩纷呈,真正体现学生的主体地位,让学生体验“发现者”和“探索者”的无穷乐趣。
二、注重一致性-------认知性评价与情感性评价
评价学生的学习,教师不仅要关注学生是否掌握了相关知识与技能,而且还要关注他们的情感、态度与价值观;学生的学习结果固然重要,但更要在意知识形成的过程以及学习过程中的情感体验。
课堂中学生知识学习过程中表现出来的强烈的兴趣、积极的态度、坚强的意志、足够的自信心、教师要及时评价决策、调整教学策略,这非常有利于学生提高自我认识、增强信心,并激发学习的动力,以更加积极的心态继续学习,顺利实现课堂教学目标、促进课堂和谐发展。
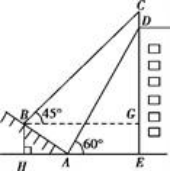 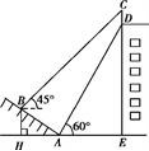 案例2: 案例2:
如图,某大楼的顶部竖有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1∶ ,AB=8米,AE=12米,求广告牌CD ,AB=8米,AE=12米,求广告牌CD
的高度。
师:大家以前见过此题吗?
生:没有。
师:请甲同学尝试解决
生甲:我不会。
师:我并不需要你完整的解答,只要你走出第一步,可以吗?
生甲:我来试一试,大概要用到解直角三角形吧!我由i=1∶
能算出∠BAH=30°,Rt△AED中,知道AE=12,∠DAE=60° ,可以算出DE=AE
tan60° =12
师:恭喜你,第一步走的不错!再努力一把,试着走出第二步。
生甲:从点B处测得C的仰角为45°,好像用不上这个度数,走不下去了!
师:看来是“山穷水尽疑无路”了
生:(附和:)柳暗花明又一村
师:(准备给予适当提示)诗接的不错!我们试着过点B作BG⊥DE于点G,看看有没有新的发现。
生甲:(有所醒悟)我能得到BG=HE,而HE=AH+AE,AH的长度可以由Rt△ABH中解直角三角形得到,具体是AH=AB
cos30°=4,这样BG也能计算出长度了。
师:很好,同学已经取得阶段性的胜利,成功的曙光即将出现。你很想求出哪条线段的长度啊?
生甲:(受到鼓励,放松了许多)若能求出CE的长度,可由CE-DE得到CD。哦,对了!可以将CE分割成CG与GE长度之和,GE=BH=0.5AB,CG可以借助等腰直角△BGC得到CG=BG。
师:开始我只要求你走一步,可你一不小心就走完全程,感觉如何?
生甲:美妙极了!确有一种豁然开朗的感觉。(全班学生鼓掌大笑)
教学随想 作为教师评价学生,我们不能总看结果,而应从是否激发了学生的兴趣,是否有效地训练了数学的思维,是否从不同角度客观的评价一个学生。在本案例中,教师对学生甲适时提示、给予评价,给全班学生会产生一种正面的效应,凸显的是“斗罢艰辛,踏歌而行”效应,增强自我磨砺,逆风而行的勇气和树立必胜的信心,体现新课程标准中“数学学习水平与情感、态度价值观的多重评价”理念。
三、评价也要“换位思考”-----单向性评价与互动性评价
课堂中,对于教师的提问,学生发表了自己的观点后,老师一般会对其见解直接评价,以激励他们作更深入的思考。整个过程可以呈现学生的主体地位与教师的主导作用,有助于促成学生把握知识的本质,领悟问题的精髓。但在一些数学问题上,层次不同、思维相异的学生考虑问题的出发点和层面都不尽相同,教师要积极鼓励中下层学生大交流,并敢于向其他同学实施评价,这不仅能够有效提高他们的主动性和积极性,更重要的是能够促进他们有效反思自己的学习和能力,有利于培养学生的解决问题的能力。再者,学生评价其他同学的过程其实也是交流的过程,是另一种学习,而年龄相仿的学生之间的启发会能够让彼此共同进步,同学在“教”别人的同时也提高了学习的效率。同学在彼此评价中,将学习成果主动分享成果,更加能认识到自己的长处与短板,有效地实现《新课程标准》中的学习“有价值的数学知识”,在数学上“得到不同的发展。”
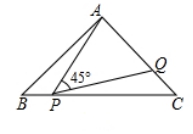 案例3: 案例3:
已知等腰直角△ABC中,∠BAC=90°,AB=AC=2,动点P在直线
BC上运动(不与点B、C重合).如图,点P在线段BC上,作∠APQ=45°,PQ交AC于点Q当△APQ是等腰三角形时,求AQ的长.
师:本题欲求AQ的长度,是从求CQ来找方法,还是通过条件“△APQ是等腰三角形”寻求突破,请大家畅所欲言,各抒己见,但要说清理由哦!
生1:△APQ是等腰三角形,到底谁是腰谁是底,我无法确定,所以就无法找到突破口。
师:无法确定就走不下去了吗?不妨找一种可能试试看!
生2:假设AP=AQ,此时∠APQ=∠AQP=45°;因为等腰直角△ABC中,∠BAC=90°,AB=AC=2,
所以∠B=∠C=45°,而∠AQP>∠C的,即∠AQP>45这与∠AQP=45°是矛盾,所以这种可能不存在。
生3:既然前面的同学把AP=AQ否定了,我们可继续讨论,当AP=PQ时,通过前面的条件能看出可得△ABP≌△PCQ,所以AB=PC=2,在Rt△ABC中,
所以BP=CQ=BC-PC=2-2,求得CQ,所以AQ=AC-CQ=2-(2-2)=4-2
生4:我很赞赏同学2的做法,通过全等这个“转换器”将CQ转换成了BP,值得我学习。
生5:继续刚才的分类,当AQ=PQ时,点Q与点C重合了,此时AQ=AC=2
生6:我注意到如果按照同学5的方法,AQ=PQ时那么∠APQ=∠PAQ=45°,此时∠AQP=90°,点Q与点C不可能重合,所以同学5应该仔细观察图形,不应该草率地下结论。
 生5:谢谢同学6的纠错!看来我需要重新画个图! 生5:谢谢同学6的纠错!看来我需要重新画个图!
生7:我画出了同学6的所提到的图形,根据同学6的分析,那么△APC是等腰直角三角形,
则∠APC=∠AQP=90°,所以AQ=PQ=QC=0.5AC=1.
师:刚才几位同学的互评互助很好的解决了这个问题,有效地利用了“分类讨论”的数学思想;同学3发现了“一线三等角全等”模型,并恰当转换,体现了“转化”的数学思想;同学6的观察力很强,同学7的快速作图能力值得表扬,看来“团队”的力量果然是巨大的。
教学随想 新课程标准推崇互动化的评价,学生这间的彼此协调沟通,不赞成教师单一评价学生,提倡结合小组互评与自评,师生互动评价,让评价在课堂中形成有效的交互。学生犯错,教师不要“一棍子”打死,更不能全盘代替学生回答与思考问题,而应有效组织他们互相评价,让学生的思维碰撞出发散的火花,创造性地解决问题,这样学生的认知水平不仅得到很大的提高,他们的探究能力与探索兴趣也会增强。
四、“评”了也应有“价”值-------激励性评价与反思性评价
课堂中教师为了贯彻“一切为了学生发展”的理念,对学生采取积极肯定的正面评价,从而可以激发学生的主动性、创造性。很多教师更擅长于运用赏识的语言评价学生,使学生体验到成功的乐趣,感受到自己的潜能,增强了学习的信心;但是滥用激励评价会让学生飘飘然,盲目自信,眼高手低;过于重视激励评价也会过犹不及,甚至适得其反;评价的目的是促其全面完整地了解知识,学会自我反思总结,从而变得更加完善。因此,恰当运用激励评价的同时更应适时进行反思性评价,引导学生主动反思,思其不足,虑其不周,并及时总结,做到自我调节,不断完善,才能最大限度地激发他们的学习热情。
案例4:
某商品的进价为每件40元,售价为每件50元,每个月可卖出210件,如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元),设每件商品的售价上涨x(x为正整数)元,每个月的销售利润为y元,每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
多数同学在解答这道题的时候,也知道先求出y与x的函数解析式,但是受到思维定势,总是想着常规方法:即将二次函数写成顶点式后,y=(210-10x)(50+x-40)=-10x2+110x+2
100=-10(x-5.5)2+2
402.5,就觉得x=5.5时,y最大值=2402.5,此时教师首先肯定其处理一般最值问题的常规方法,接着就可以引导全班同学积极参与讨论,彼此启发补充,关注到题目中的“0<x≤15,且x为整数”这个条件,经过及时修正调整,进而不断完善得到正解的解法: a=-10<0,所以当x=5.5时,y取得最大值2402.5;
因为0<x≤15,且x为整数,所以当x=5时,50+x=55,y=2400;所以当x=6时,50+x=56,y=2400.
所以当售价定为每件55元或56元时,每个月可获得最大利润,最大的月利润是2400元。
教师适时点拨,激励同学自己主动探索,不断发思,大胆尝试,即使失败,也要找出原因,这样才能得到更加深刻的理解。
教学随想 本案例中,学生的错误认识往往就体现了他自己的真实思维,对待这种错误,教师的评价应避重就轻,找出其闪光点进行激励性评价,促其反思自己解决问题中的不足之处,痛定思痛才能凤凰涅槃获得成功。学习中,更要把他人的评价与自我反思相结合,方能真正提高自我的分析能力,教师的评价,通过自己的反思,才能转变成自己的能力与智慧。
初中数学对学生的学习意识、思维灵活有着更高的要求,评价直接影响学生的思维训练与学习兴趣。多元评价不同于单向评价,评价更不等同于评分,让评价真正走进学生的内心世界,为学生营造一个和谐沟通的世界,促进学生最大的发展。
参考文献
[1]马云鹏:《数学教育评价》, 高等教育出版社
[2]黄衍顺:《在初中数学教学中通过多元评价促进学生的发展》,《新课程·下旬》, 2013 (4)
|